Subsections
Global Illumination is the term given to models which render a
view of a scene by evaluating the light reflected from a point 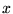 taking into account all the that arrives at that point.
Consideration is give not only to light arriving directly from
light sources but from all indirect illumination due to light
interacting with other objects.
taking into account all the that arrives at that point.
Consideration is give not only to light arriving directly from
light sources but from all indirect illumination due to light
interacting with other objects.
Local reflection models deal with direct illumination only,
ignoring interactions with other objects and required add-on
algorithms to handle effects such as shadows, reflections and
transparency. Global methods can handle these phenomena
inherently.
The two established global algorithms are raytracing and
radiosity. Neither is a complete solution. Raytracing attempts to
render perfect11.1 specular reflection. Radiosity deals
with the more difficult problem of diffuse11.2 interaction.
The essential difference between the implementation of the two
methods is that raytracing traces ray from the pixel into the
scene back to the light sources, while radiosity follows light
from light sources through the scene as patch-to-patch diffuse
interaction. The radiosity solution needs to be passed through a
traditional visibility process to deal with projection and Hidden
Surface Removal .
Radiosity was developed from systems designed to model the
transfer of heat in closed systems, but was adapted to deal with
light transfer. Radiosity considers the diffuse interaction
between 'patches'(polygons) in the scene. Because diffuse
reflection is not view-point dependant (unlike specular
reflection), the radiosity solution is view-independent. This has
two important consequences.
- Radiosity needs to be calculated for all points in the
scene rather than just the points visible to the viewer.
- Once a solution is calculated, that solution remains valid
for all viewpoints as long as the scene doesn't change.
Figure 10.1:
Cornell Box, the "Hello World" of
Radiosity
|
|
Diffuse reflection occurs when light strikes surface and that some
light is reflected (equally in all direction) This reflected light
is called radiance. Any given surface in a scene is
irradiated (receives light) and radiates light. The core of
radiosity is calculating how light radiated from one surface
illuminates another surface.
Initially the scene is divided into a number of flat patches.
Light sources are considered as light emitting patches. Light is
'shot' from the sources into the scene and 'stored' by different
patches in varying amounts, depending on their distance and
orientation.
Each patch will radiate some of the absorbed light back into the
scene (the exact amount will depend on surface properties. The
patch with the highest unradiated light then shots its light back
into the scene to be stored by other patches. The patch with the
next highest stored light is processed. This continues until a
very high proportion on the original light has been distributed.
At any stage, some of the light will arrive back at patches which
have already been considered. This implies that the process needs
to be iterative. Between 20 & 500 iterations are needed.
The transfer of light between any two patches is calculated using
the geometric relationship between the two patches, this
relationship is known as the form factor. The form factor
determine what proportion of light emitted by a patch will arrive
at another patch. The form factor needs to be calculated for every
pair of patches in the scene (i.e is a scene contains 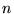 patches,
patches,
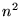 form factors are needed. The form factor also needs to take
into account the presence of any intervening patches.
form factors are needed. The form factor also needs to take
into account the presence of any intervening patches.
The cost of radiosity depends on the square of number of patches
in the scene (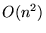 ). To keep processing costs down, the
patches are made large and the light intensity across a patch is
assumed constant. However is introduces problems where there is an
illumination discontinuity across a patch (e.g a shadow). To
resolve this problem, a patch needs to be subdivided if there is a
discontinuity across the patch.
). To keep processing costs down, the
patches are made large and the light intensity across a patch is
assumed constant. However is introduces problems where there is an
illumination discontinuity across a patch (e.g a shadow). To
resolve this problem, a patch needs to be subdivided if there is a
discontinuity across the patch.
Figure 10.2:
Subdivision of the Cornell Box
|
|
In order to determine which patches need to be subdivided and by
how much, a process known as progressive refinement is
adopted. This process generates progressively accurate images. The
progressive refinement procedure involved iterating the radiosity
process subdividing patches each time. At each iteration new form
factors need to be calculated and the radiosity begins again.
To calculate the form factor between a patch and the remainder of
the scene, a hemicube is placed onto the center of the
patch. This hemicube is divided into a number of
pixels11.3. Other
patches are projected onto the sides of this hemicube, with the
center of the original patch acting as the center of projection.
The number of 'pixels' onto which a patch has been projected will
determine the form-factor. Where two or more patches project onto
one pixel, a Z-buffer type approach is used to determine which is
the nearest.
Figure 10.3:
Projecting a patch onto a hemicube
|
|
There are 3 significant problems with radiosity rendering.
- Algorithm Artifacts Certain assumptions and approximations
necessary for radiosity can cause visual problems such as Mach
Banding in a scene.
- Specular Reflection Radiosity deals only with diffuse
reflections, hence does not render Specular reflection at all.
Most radiosity systems, incorporate a final 'Raytracing pass' to
overlay specular effects on the final image.
- Rendering Time The calculations of forms factors and the
iterative nature of radiosity make the method unsuitable for
real-time rendering.
powerk
2004-07-14

![]() patches,
patches,
![]() form factors are needed. The form factor also needs to take
into account the presence of any intervening patches.
form factors are needed. The form factor also needs to take
into account the presence of any intervening patches.