Scanline HSR

Last Updated March 5, 2013

The Scan-Line HSR Method

This HSR technique processes the scene one scan-line at a time. For each scan-line in the window, we must determine which polygons the scan-line intersects. Then for each pixel along the scan line, determine which polygon is nearest the eye at that point; this then determines the colour of that pixel.

Because the scan-line method draws the image scan-line by scan-line, some pre-processing of the polygon mesh is required before rasterization.

Horizontal Edges must be removed, these edges will be drawn when the adjacent edges are processed.
The algorithm uses edge crossing to detect entry and exits of polygons. Each edge crossed changes the "inside-outside parity" When a scan-line passes through the end-point of an edge, it produces two intersections, one for each edge that meets at that vertex. This is OK if the vertex is a local minimum or maximum. If the vertex is not a local extremum, the two intersections will cause the parity to be unchanged. To resolve this problem, when an intersection is not an extremum, simply reduce the $y_{upper}$ co-ordinate of the lower line segment by 1. This will not effect the accuracy of the method as we will use to slope of the line segment before shortening.

To keep track of which polygons we are currently drawing we need to build an edge table, which contains an entry for each scan-line, this entry is a list of all edges first intersected by a given scan line. Each edge contains some information about the edge and a list of associated faces (polygons).

We also need an Active Edge List (AEL) which contains a list of edge nodes. The AEL represent edges intersected by the current scan line. The AEL needs to be maintained as we move from on scan-line ( $y$ ) to the next scan-line ( $y+1$ );

Some of the edges in the AEL will no longer be intersected by $(y+1)$ . Remove all edges from the AEL, where $y_{upper}$ is less than $y+1$ .
The intersection point of the scan line with the remaining edges will change for the new scan-line. $x_{int}$ is updated to $x_{int} + y_{m}$ . Note that $x_{int}$ must be stored as a real number to avoid round-off errors.
New edges may need to be added to the AEL. If $y+1$ is equal to $y_{lower}$ of any edges in the edge table, then those edges must be added to the AEL.
The node in the AEL must be sorted (for parity checking) in ascending order of $x_{int}$ , so, after adding new edges and updating $x_{int}$ values of the edges, the AEL must be sorted.

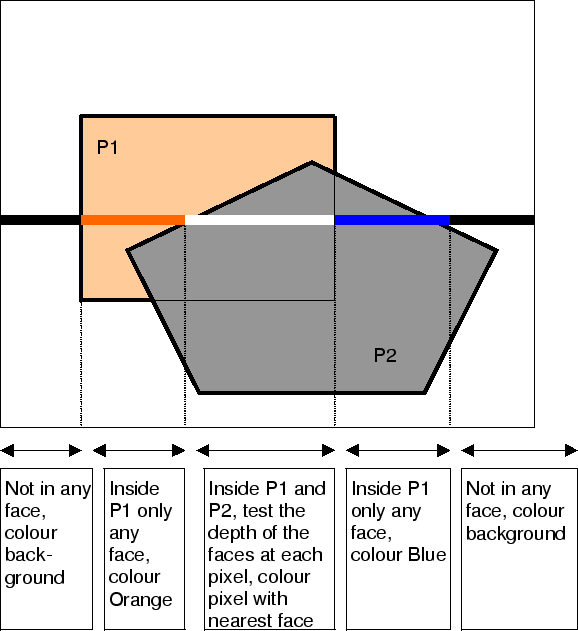
For each polygon in the scene, we maintain a flag which is set IN or OUT depending on whether we are inside or outside that polygon. As we process a scan line, we will cross edges, as we cross an edge we must 'reset' the flag for each polygon which shares that edge. If we are IN a polygon and we pass an edge of that polygon we must reset the flag to OUT. As we process a scan-line, pixel by pixel, we need to colour the pixels as follows.

If no flags are set to IN then the pixel gets background colour.
If only ONE flag is set to IN, the pixel gets the colour of face we are in.
If more than one flag is IN, we need to determine which face is closest at that point by calculating the depth of each face as in the Depth Buffer method. The pixel gets the colour of closest face.

When we are IN two or more polygons, we can calculate the closest face for each pixel or we can assume that the closest face at the first pixel of the overlap will remain the closest face until we meet another edge. This way we need only calculate depths at the beginning of an overlap area and need not do the calculations for every pixel. This will allow us to implement a very efficient algorithm, which fills pixel runs between edges. However this optimization will not work for some scenes.