Last Updated
March 5, 2013
Scanline Triangle Filling (simplified for single triangles)
This technique fills polygons one scan-line at a time.
For each scan-line in the window, we must determine which
polygons the scan-line intersects.
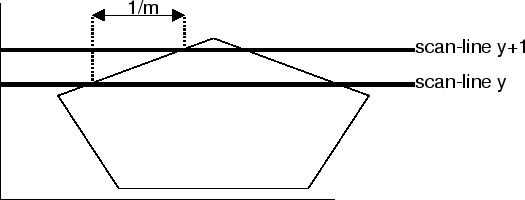
The scan-line method takes advantage of edge coherence, i.e.
- Many edges that are intersected by scan-line
$y$
are also
intersected by scan-line $y+1$.
- The x-value of the point of scan-line intersection migrates
predictably from scan-line to scan-line. The x co-ordinate of the
intersection of an edge with a scan-line increases by
$\frac{1}{m}$
for each scan-line, where
$m$
is the slope of the
edge.
An important component in the data structure needed for this
algorithm is the edge node. Each edge in the polygon is represented by an edge node. An edge node contains
the following information;
-
$y_{upper}$
, the
$y$
co-ordinate of the upper end-point of the edge.
- $y_{lower}$
, the
$y$
co-ordinate of the lower end-point of the edge.
-
$x_{int}$
, initially the
$x$
co-ordinate of the lower end-point of the
edge. As the algorithm progresses, this field will store the
$x$
co-ordinate of the point of intersection of the scan-line.
-
$y_{m}$
, the reciprocal of the slope of the line (
$\frac{1}{m}$
).
When constructing an edge node for the edges, the following must be taken into account;
- Horizontal Edges are ignored (an edge node is not generated for these), these edges will be drawn
when the adjacent edges are processed.
- If two edges share a vertex AND the vertex is an upper end point for one edge and a lower end point for another edge, the $y_{upper}$ of the lower edge must be reduced by $1$.
We also need an Active Edge List (AEL) which contains the two edge nodes with the lowest
$y_{lower}$
. The AEL represent the two edges intersected by the current scan line. The AEL needs to be maintained as we
move from on scan-line
$y$
to the next scan-line
$(y+1)$
;
- Add any edges whose $y_{lower}$ is equal to $y$ .
- Fill the pixels from the
$x_{int}$
of one edge to the
$x_{int}$
of the next.
- One or both of the edges in the AEL will no longer be intersected by
$(y+1)$
. Remove the edges from the AEL, where
$y_{upper}$
is equal
to
$y$
.
- The intersection point of the scan line with the remaining
edges will change for the new scan-line.
$x_{int}$
is updated to
$x_{int} + y_{m}$
. Note that
$x_{int}$
must be stored as a real
number to avoid round-off errors.
- increment y (to the next scan line)
- Repeat until the Edge List and AEL are empty.
© Ken Power 1996-2016