Last Updated April 19, 2010

Backface culling

Before the scene is rendered, polygons (or parts of polygons) which will not be visible in the final scene. Three types of polygon removal are required;

Removing backfaces (faces turned away from the camera)
Clipping faces against the view volume
Remove faces or parts of faces that are hidden behind other parts of the model (hidden surface problem).

This page examines the first type of polygon removal (backface culling).

Backface Culling

Each face of a sold polyhedron has two sides, a frontface on the outside and a backface on the inside. We can only see frontfaces, and normally, we can only see about half of the front faces. If we take one polygon in isolation, and find that we are looking at it's backface, we can cull that face (remove that face from the list of faces to be rendered).

Only half of this polyhedron's 12 faces are normally visible

We need to check each polygon on the model to see if it is visible (if it is a frontface). There are two approaches to determining if a face is a front or backface.

Signed area of triangle

Recall that the cross product of two vectors gives a new vector. The length of this new vector is equal to the area of the parallelogram formed by the vectors, or twice the area of the trangle formed by the vectors.

For a triangle $V_0,V_1,V_2$, we can find two vectors along the edges by finding the displacements between the vertices (see diagram);

$\vec{v}=V_{1}-V_{0}, \vec{w}=V_{2}-V_{0}$

Calculate the area of the triangle $V_{0}(2,2),V_{1}(5,3),V_{2}(3,4)$, then calculate $V_{0}(2,2),V_{1}(3,4),V_{2}(5,3)$.

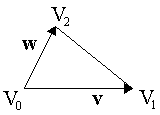
So the area of the triangle is ${Area}_{\triangle}=\frac{1}{2}\|\vec{v}\times\vec{w}\|$. For a 2D triangle (e.g. a triangle in screen space, assuming the z-ccords are zero), the area can be calculated as;

\[ {Area}_{\triangle}=\frac12((x_{1}-x_{0})(y_{2}-y_{0})-(x_{2}-x_{0})(y_{1}-y_{0}))\]

Note that this area will be positive if $V_{0}V_{1}V_{2}$ are oriented counterclockwise around the triangle and negative if the triangle is clockwise.

This technique will only work if the triangles are consistently defined with counter-clockwise winding when viewed from the outside. If we measure the area of such a triangle and find it to be $<0$, then we know we are looking at a backface which doesn't have to be drawn.

Left: no faces culled, right: backfaces culled

Using the Normal

If we know the outward normal to a face, we need to choose any point $\vec{q} $ on the face.

Determining a Backface

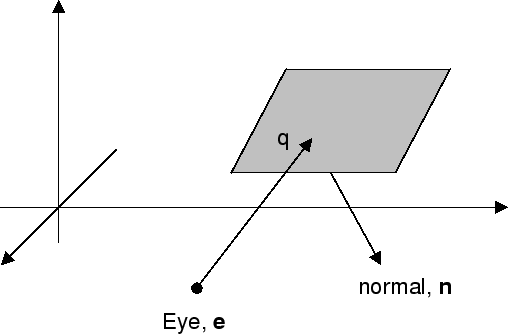
We are interested in the angle $\theta$, between the vector $(\vec{e} -\vec{q} )$ and the normal vector $\vec{n} $(figure below). If this angle is greater than $90^{\circ}$, then the face is a backface (the face is oriented away from the eye). We can perform this test with a simple dot product, the dot product of two vectors is related to the angle between them. A face is a backface if the following holds true:

\[ \vec{n} .(\vec{e} -\vec{q} )<0 \]

If this expression is zero then the face lies parallel to the line of sight and is therefore visible.

We can now process the model to remove the backfaces, typically removing backfaces will halve the number of polygons to involved in further processing.

caption

Backface culling in OpenGL.