Shading methods (left to right); Flat
shading, Smooth shading no specular, Smooth shading f=20, Smooth
shading f=200
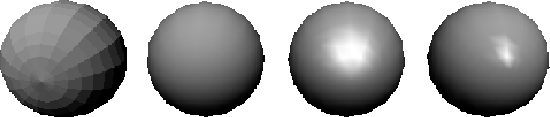
Last Updated April 19, 2010
Polygon mesh models are distinguished by the fact that the model only approximates the actual objects represented. A Shading model must apply some reflection model (e.g. Phong reflection) to these faces, in order to determine how the face is to be colored. The reflection model should take into account orientation of light sources, position of viewer and properties of the surface being rendered. Polygon meshes are typically collections of planer faces, which model smooth surfaces. Combining diffuse and specular reflection models, we get the following model for light intensity at a point on a surface
\[ I=\underbrace{\mathstrut I_{a}R_{d}}_\textrm{ambient}+ \sum_{i=1}^{\mathrm{lights}} \left( \underbrace{\mathstrut I_{s_{i}}R_{d}(\vec{N}\cdot\vec{S_{i}})}_\textrm{diffuse}+ \underbrace{\mathstrut I_{s_{i}}R_{s}(\vec{R_{i}}\cdot\vec{V})^{f}}_\textrm{specular} \right) \]
A naive Flat Shading technique will apply a refection model to one point on a face and the shade determined is applied to the entire face. This method is quick and produces acceptable results if smooth surfaces are not involved. Specular reflection will be shown in flat shading, but only very coarsely. If realistic scenes are to be generated, flat shading requires so many polygons as to be infeasible. Regardless of the number of polygons, flat shading will almost always give a faceted appearance (figure below) in certain areas because of Mach Banding , which tends to exaggerate the differences between faces. Flat shading is generally only used for prototyping or testing an application where speed, not accuracy is important. Other methods can produce more realistic displays with much fewer polygons.
In order to accurately render curved surfaces represented by a polygon mesh, we need to implement an Incremental or Smooth Shadingtechnique to smooth out the faceted nature of the mesh. The first smooth shading technique developed was Gouraud Shading.
This method simply calculates the Surface Normal at each vertex by averaging the normals of the faces which share the vertex .
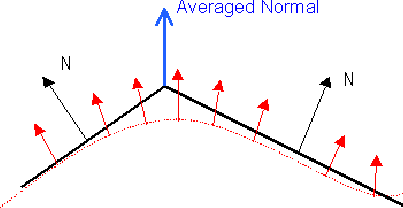
This average normal will coincide closely with the normal of the actual modelled surface at that point. This vector is then used in a reflection model to determine the light intensity at that point. This process is repeated for all vertices in the model. Once the correct intensity has been calculated for each vertex, these are used to interpolate intensity values over the face. The interpolation scheme is know as bi-linear interpolation.
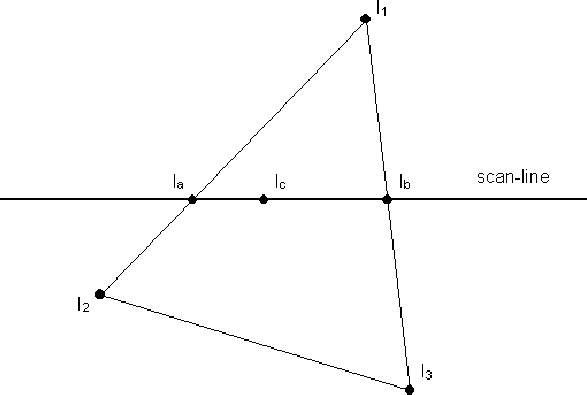
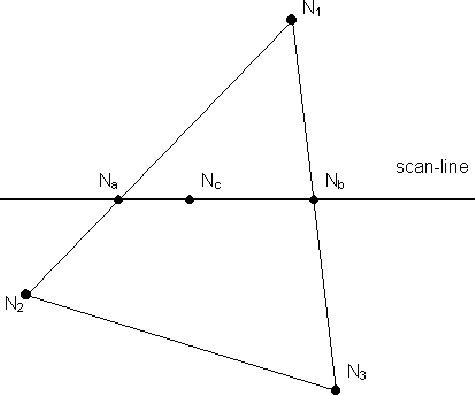
In the figure above, intensities are known for $I_{1}$ , $I_{2}$ and $I_{3}$ . $I_{a} $ and $I_{c}$ can be interpolated as follows:
\[\begin{eqnarray*} I_{a}=I_{1}+(I_{2}-I_{1})\frac{y_{a}-y_1}{y_2-y_1}\\ I_{c}=I_{a}+(I_{b}-I_{a})\frac{x_{c}-x_a}{x_b-x_a} \end{eqnarray*}\]Gouraud smoothes the faceted appearance of meshes, because the interpolated intensities along an edge are used to shade both polygons which share that edge. This means that there is not a discontinuity of colour at the edges of adjoining faces.
However, although the mesh appears smooth, the polygons are still visible at the edge of the object when viewed as a silhouette. Gouraud can also interpolate incorrectly which results in some rendering errors which remove some detail.
The biggest problem with Gouraud shading is the fact it reproduces specular shading poorly and if specular reflection is displayed, it is determined by the polygon mesh rather than the modelled surface. If a highlight occurs in the middle of a polygon, but not at any of the vertices, the highlight will not be rendered by interpolation. Also, Mach banding can occur when specular refection is incorporated into Gouraud, for this reason, the specular component is often ignored when using Gouraud, giving 'smother' results.
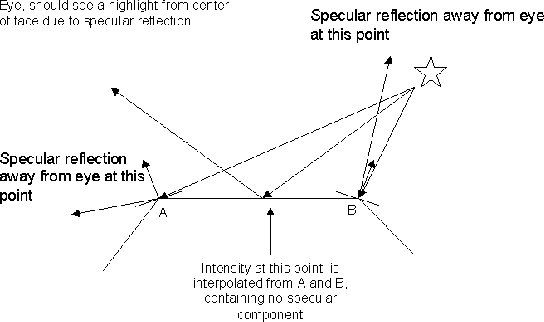
Phong shading overcomes the problems of specular reflection encountered in Gouraud shading. This method again calculates the normals at the vertices by averaging the normals for the faces at that vertex. These vertex normals are then interpolated across the face.
Thus we have a good approximation of the surface normal at each scanline position (pixel) and therefore we are able to calculate more accurately the intensity at that point, including specular highlights. The interpolation scheme for normals, is similar to Intensity interpolation.
>
Phong shading requires intensity calculations at each point on the face, so is therefore far more expensive that Gouraud which only performs intensity calculations at the vertices. Note that the computation of normals in both Gouraud and Phong must be done in world coordinates, as pre-warping distorts the relative orientation between surface, light-source and eye. Both these methods can be integrated with Z-Buffer or scanline filling algorithms.
© Ken Power 1996-2016