Last Updated October 16, 2013
A point is an exact location in space.
Two points form a unique line segment. It is the straight path between both points.
A triangle is made by connecting 3 points with line segments.
Will a triangle in 3D be a triangle when converted to 2D ?
Will the shape of a triangle change when converted to 2D?
You can think about the points, lines, and plane figures that compose the 3D scene without using a coordinate system. In fact, that is what we have been doing. But in computer graphics we need to represent these objects, somehow, and to manipulate them. To do this, we need a method to represent such objects.
Pick a convenient point in the 3D scene and call it the origin. Now define three lines called X, Y, and Z that go through the origin. Usually the three lines are perpendicular to each other. Each line is called an axis.
Pick a positive direction for each line. There are several choices here, but let's make the choice shown in the picture.
Now each point of the X axis is a unique distance (positive, negative, or zero) from the origin. For example, the corner of the building that lies on the X axis is at a distance of 8.0 feet (or so) from the origin.
Any point in our 3D scene can be assigned a representation by measuring its distance along the three axes. For these notes (and for many computer graphics books), these three distances are put into a column matrix as follows.
You are probably accustomed to putting the three coordinates into a triple such as (x, y, z). But it will turn out that for computer graphics it is more convenient to put them into a column, as above.
For example, the coordinates of the corner of the building that lies along the X axis are (about):
The coordinate frames used in math books are not usually placed in a real world scene, so the distances are not expressed in any particular unit. When you create your 3D world inside a computer you need to decide on the units you are using. 
The picture shows our 3D world with a different coordinate frame placed in it. The points in the world are the same points as before. But now, with a different coordinate frame, they will have different representations.
In the previous frame, the point labeled P1 was given the representation:
Now, the distances along the axes in the new (green) frame are different. The column matrix that represents P1 in the new frame is roughly:
As you look at the building, Light is flooding in from a direction behind you and to the upper left. The picture represents this sunlight as arrows. Although the picture is 2D, try to think of the 3D scene. The direction an arrow is the direction in which the light is traveling. The length of the arrow (let us say) represents the intensity of the light.
The direction of the light and its intensity can be represented as a vector. A vector is a geometrical object that has two properties: length and direction. Light from the sun has two properties: brightness and direction (we are disregarding colour information.) Make the length of the vector proportional to the brightness of the light.
Wind, also, is represented as a vector. Wind has direction and speed. A particle of dust travels in the direction of the wind. The length of the vector is proportional to the speed of the dust particle.
A vector does not have a position. The picture shows several arrows that represent the flood of light coming in from the sun. But the arrows could have been drawn anywhere as long as their direction and length was the same.
A vector is represented with a column matrix (as are points). It is somewhat confusing that both points and vectors are represented with the same thing. But this will prove to be convenient for computer manipulation.
To represent a vector as a column matrix:
A convenient way to do this is to position the tail of the vector at the origin, and then just read off the x, y, z values at the tip.
So the vector that gives the intensity and direction of sunlight in the picture is:
The column matrix represents the vector using our chosen coordinate frame. The column matrix is not the vector. If we had picked a different coordinate frame, the vector in the physical scene would be the same, but its representation using the new frame would change.
It is useful to have names for matrices. Usually a bold lower case letter is used for a column or a row matrix:
a = ( 1.2, -3.6 ) x = ( x1, x2, x3, x4 )
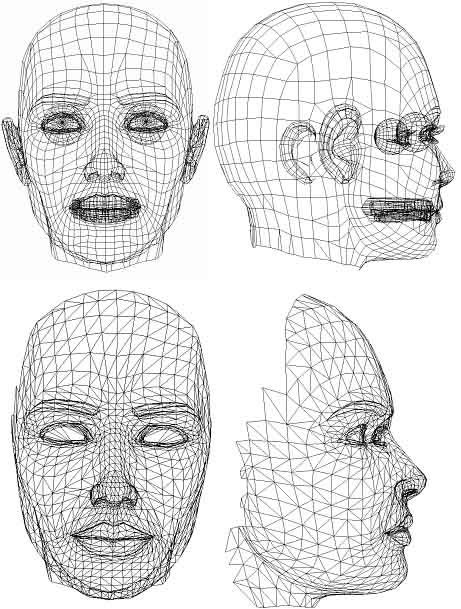
Hundreds of points, lines and triangles can represent an object.
If we move from one point to another we move it a certain distance in a certain direction. The combination of distance and direction is called Displacement. The displacement is usually represented by a vector. The displacement is distance and direction, so a certain displacement can be applied to many different points.
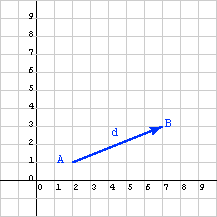The figure shows a displacement vector representing the difference between two points in the x-y plane. (For now, the examples are in two dimensional space; three dimensional space will come later).
Computing the displacement from A to B can be done as two separate problems:
The displacement vector expressed as a matrix is:
d = (5, 2)
Displacement vectors are often visualized as an arrow connecting two points. In the diagram point A is the tail of the vector and point B is the tip of the vector. (However, recall that vectors do not have a position, so this is just a convenient place to draw it, not where it is.)
We can write the displacement as; d= pointA - pointB (note subtracting two points gives a vector)
Addition is done by adding corresponding elements of the input matrices to produce each corresponding element of the output matrix.
( 1, 2, 3 ) + ( 10, 20, 30 ) = ( 11, 22, 33 ) ( 42, -12 )T + ( 8, 24 )T = ( 50, 12 )T ( 9.2, -8.6, 3.21, 48.7 ) + ( -2.1, 4.3, 1.0, 2.3 ) = ( 7.1, -4.3, 4.21, 51.0 ) ( 32.98, -24.71, 9.392 )T + ( -32.98, +24.71, -9.392 )T = (0, 0, 0)T
If a and b are matrices of the same type, then a + b = c means that each element ci = ai + bi
Is Matrix addition commutative ?
a + b same as b + a?
Is Matrix subtraction commutative ?
a - b same as b - a?
The negative of a matrix is this:
-a means negate each element of a.
So, for example:
-(22, 5, -12 ) = ( -22, -5, 12 )
Vectors are geometric objects. A particular vector can be represented in a variety of ways. It is important to understand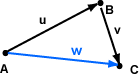
the difference between a geometric object (such as a point or a vector) and the way it is represented (often with a column matrix).
The diagram shows points A, B, and C (in two dimensions). A displacement is a distance and a direction. Vector u is the displacement from A to B. Vector v is the displacement from B to C.
The displacement from A to C is the vector w. The effect of moving through the displacement u and then through the displacement v is the same as moving through the displacement w. In symbols:
u + v = w
Head-to-Tail Rule: Move vector v (keeping its length and orientation the same) until its tail touches the head of u. The sum is the vector from the tail of u to the head of v.
Points can be represented with column matrices. To do this, you first need to decide on a coordinate frame (sometimes called just frame. A coordinate frame in consists of a distinguished point P0 (called the origin) and an axis for each dimension (often called X and Y). In 2D space there are two axes; in 3D space there are three axes (often called X, Y, and Z).
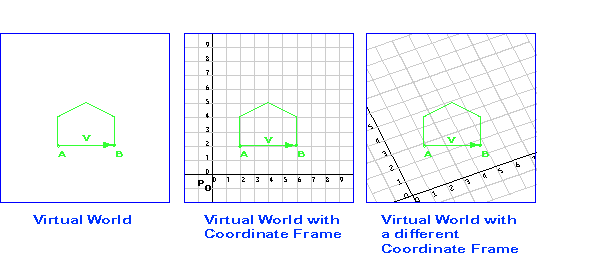
For now, let us talk about 2D space. The left diagram shows a (rather simple) virtual world in 2D space. The points and vectors exist in the space independent of any coordinate frame. The next diagram shows the same virtual world, this time with a coordinate frame consisting of a particular point P0 and two axes. In this coordinate frame, the point A is represented by the column matrix (2, 2)T.
The right diagram shows the same virtual world, but with a different coordinate frame. In the second coordinate frame, the point A is represented by the column matrix (2, 3)T.
What frames of reference do we use in everyday life?
What happens if we add a vector and a point?
Sometimes the operation of adding a vector to a point is called translation. The original point is sometimes said to have been "translated to a new location."
The vocabulary here might be confusing. In mathematical terms, the sum of a vector and a point yields a new point. The first point remains unchanged. But in computer graphics terms it is nice to think about pictures "moving across the screen" when displacement vectors are added to their points. So sometimes people talk about "moving a point" and talk about the "old point" and the "new point".
How long is a vector?
Easy for axis aligned vectors.
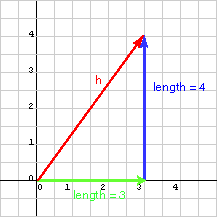
length of $(x,y)=\sqrt{x^{2}+y^{2}}$
Symbol for length of vector $\vec{a}$ is $\|\vec{a}\|$
Can you have a vector with negative length?
What is the length of -a?
A 2D vector that is aligned with a coordinate axis, as with (4,0)T, has an orientation that is easy to see. It is 0 degrees, 90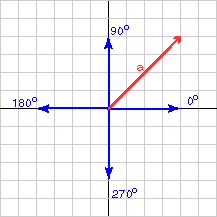
degrees, 180 degrees, or 270 degrees.
The orientation of a vector is usually expressed as an angle with the positive x axis of a coordinate frame. There are two ways of doing this:
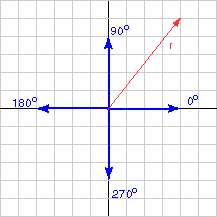
The slope of a is
(change in y)/(change in x) = 4.0/4.0 = 1.0.
So the angle is arctan( 1.0 ) = 45.
 |
 |
Vectors have no location, so neither the length nor the direction depend on where you draw a vector. The formula for the direction of a 2D vector is
$\textrm{angle of (x,y)}=\arctan(\frac{y}{x})=\tan^{-1}(\frac{y}{x})$
arctan( z ) means "find the angle that has a tangent of z." When you do this with a calculator, remember that the answer may be in radians or in degrees. Most calculators give you the option of using use either format.
Length and Direction converted to (x, y) coordinates
Say that you have been given a length and a direction and want to express them as a 2D column vector.
A vector can be stretched by multiplying its components by a real number (called a scalar).
e.g. 2a=(2ax,2ay)
Scale by a fraction....
Scale by a negative...
Scale by zero...
Can we scale a vector so that it's length is exactly 1? What should the scalar be?
This is called normalization.
When working with vectors it is often useful to know the angle between two vectors. This can be calculated using the dot product.
The dot product is;
\[\begin{eqnarray*} \vec{a}\cdot\vec{b}=|a||b|\cos\theta\end{eqnarray*}\]In this case $\theta$ is the angle between the two vectors.
What is the dot product of two perpendicular vectors?
Is $\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}$ ?
If we know the dot product of two vectors then the angle between them is
\[\begin{eqnarray*} \theta=\arccos(\frac{\vec{a}\cdot\vec{b}}{|a||b|})=\cos^{-1}(\frac{\vec{a}\cdot\vec{b}}{|a||b|})\end{eqnarray*}\]What is the dot product of a vector with itself?
There is another way to calculate the dot product;
\[\begin{eqnarray*} \vec{a}=\left( \begin{array}{c}a_{0},a_{1}\end{array}\right) \\ \vec{b}=\left( \begin{array}{c}b_{0},b_{1}\end{array}\right) \\ \vec{a}\cdot\vec{b}=a_{0}b_{0}+a_{1}b_{1} \end{eqnarray*}\]This equation also works in 3 dimensions;
\[\begin{eqnarray*} \vec{a}=\left( \begin{array}{c}a_{0},a_{1},a_{2}\end{array}\right) \\ \vec{b}=\left( \begin{array}{c}b_{0},b_{1},b_{2}\end{array}\right) \\ \vec{a}\cdot\vec{b}=a_{0}b_{0}+a_{1}b_{1}+a_{2}b_{2} \end{eqnarray*}\]What is the dot product of two normalized vectors?
The cross product of two vectors is an operation which can only be applied to vectors in 3-dimentions (and higher). The cross product takes 2 vectors and produces a 3rd vector at right angles (orthogonal) to the two original vectors.
The cross product is written as
$\vec{u}\times\vec{v}=\vec{n}$
Two points can define a line. In 3D two vectors can define a plane (a plane being a flat surface extending to infinity)
The cross product of two vectors defines a new vector which lies at right angles to the plane. There are two possible directions for a vector perpendicular to the plane. We use the "right hand rule" to figure out which direction the cross product will be.
The length of the cross product depends on the "perpendicularity" of the two original vectors.
$|\vec{u}\times\vec{v}|=\left|\vec{u}\right|\left|\vec{v}\right|\sin(\theta)$
This length corresponds to the area of the parallelogram formed by the two vectors.
What is the area of the parallelogram when the vectors are parallel?
A common requirement in programming is to be able to find a value that is between two other values, for example, find the value, x, halfway between a and b;
That is, we get the average for a & b. But what about a value that is $\frac{1}{3}$ of the way between a & b?
\[\begin{eqnarray*} x=a+\frac{1}{3}(b-a) \end{eqnarray*}\]In general, is we want to find a value that is some fraction(t) of the way between two values a & b, the equation is;
Using this equation is called linear interpolation (some times called Lerp). In this case we have 1-dimensional linear interpolation and we are interpolating along the number line (hence "linear"). Interpolation means constructing new data or values between two known values. Often this is called "tweening". Later we will look at linear interpolation in 2 dimensions, by interpolating between points on the plane.
Linear (& bi-linear) interpolation is use in many different computer graphics situations.
If we have two points, there exists one line which passes through both points. The displacement between the two points can be calculated as vector. Note that $P_{2}=P_{1}+\vec{s}$ .
The vector $\vec{s}$ can be used to generate points on the line through P1 & P2.
In general, any points on the line through the points P1&P2 can be written as;
\[\begin{eqnarray*} P_{1}+t\vec{s} \end{eqnarray*}\]where t is a real number. Here t is a special kind of variable, called a parameter. Hence these kind of equations are called a parametric equations The full parametric equation for a line is is written as;
\[\begin{eqnarray*} L(t)=P_{1}+t\vec{s}\\ \textrm{so for example;}\\ L(0.5)=P_{1}+0.5\vec{s}\end{eqnarray*}\]
Parametric equations are very useful as they can be decomposed into individual dimensions, giving the x or y coordinate;
Measure how well you understand vectors by answering these questions.
© Ken Power 1996-2016
