Last Updated March 13, 2008

Introduction to Sound

Anatomy of a Sound

adapted from James Boer, Game Audio Programming, Ch.1

Audible noise (sound) is generated by physically vibrating material. The vibration produces pressure wave in the air, the pressure wave travel through the air, and ultimately cause our eardrums to vibrate. The vibration of our ear drums is converted into electrical pulses sent to the brain, which perceives the sound.

It is the physical characteristics of the pulses which defines the aural properties of the sound.

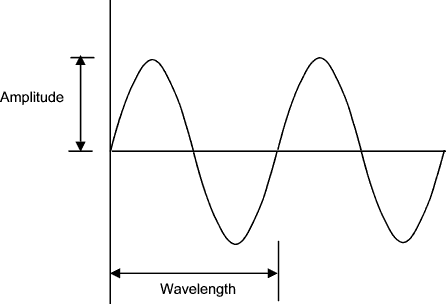
If the pressure pulses have the same attributes as a sine-wave then the sound is perceived as a single tone. In the diagram below, the x-axis represents time,and the y axis represents air pressure at a single point in space. We can interpret this diagram as showing the air pressure rising above ambient, then falling below ambient, and rising again, as the pressure pulses pass a given point.

The sine wave as two important properties;

Amplitude, describes how high the graph rises (or falls) above the x-axis. This is just another way of talking about how high the air pressure rises at the peak of each pulse. The bigger pressure difference between the crest and the through, the more movement it cause in the eardrum. Higher amplitude normally means a perceived louder sound.
Wavelength, this is a period of time in which the pressure pulse stats to repeat itself. More often we want to talk about frequency, which is the number of time the pattern repeats over a second. Frequency is measured in Hertz(Hz). Human ears can only hear sounds in the 20Hz to 20,000Hz range

frequency=¹/_wavelength

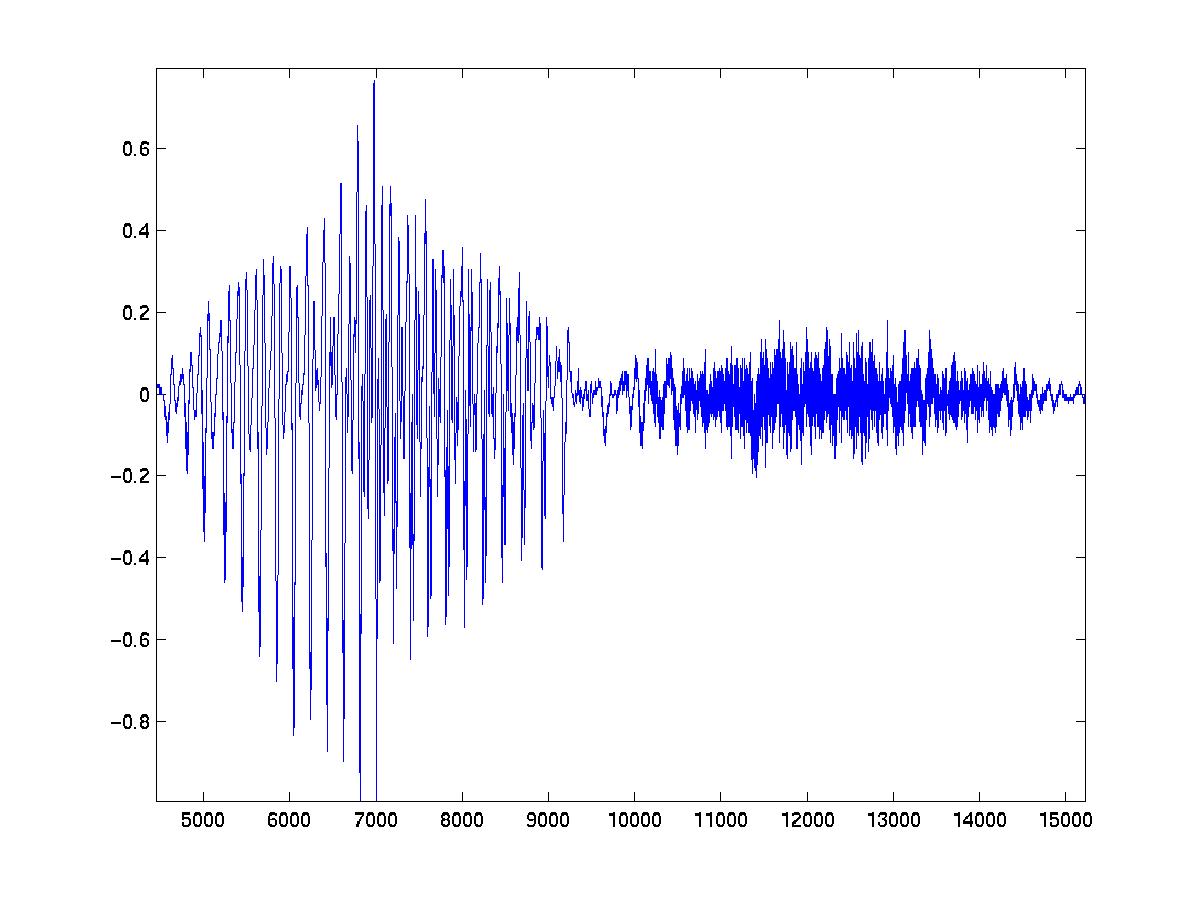
Of course not all sound is perceived as a single tone, real world sounds are much more complex. Below is a sample of a person speaking the word 'yes'. Note the 'ye..' has a higher average amplitude than the '..s', but the 's' has a much higher frequency.

Sampling

In order for computers to work with analog sound, it first needs to be converted into a digital form. This conversion process is called sampling. The most common method of sampling is Pulse Code Modulation(PCM). The two most important sound file formats, WAV and MP3 are encoded using PCM. The main difference between WAV's & MP3 files, is the MP3s are also compressed using a lossy compression algorithm.

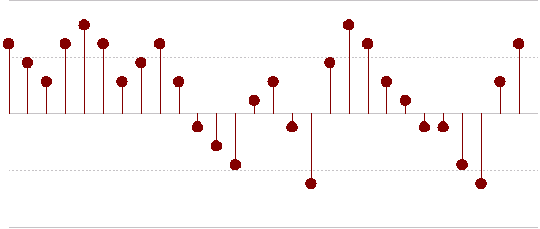
PCM involves measuring the amplitude of the audio signal at regular intervals. In the diagram below, the height of the signal is measured (red dots) at a fixed number of samples per second. Audio is normally measured somewhere between 4,000 and 192,00 samples per second.

Sampling a signal using PCM

An audio sample is then stored as a sequence of numbers, each number representing the amplitude at a given time.

The resulting sample

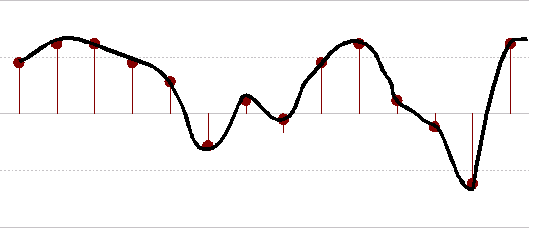
The most important factor when sampling, is the sample rate (also measured in Hertz). the number of time per second the sample is measured. In the next diagram, the sample rate is lower than the previous example. The gaps between samples is fairly large, so some of the peaks and troughs are missed.

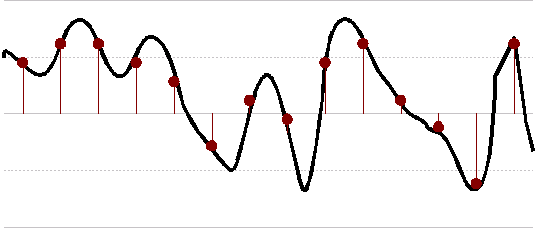
Sampling a frequency at too low a sample rate

When the audio is reconstructed from the sample, the sound produced is somewhat different from the original sound. This is due to undersampling.

Reconstructing the signal using an under sample

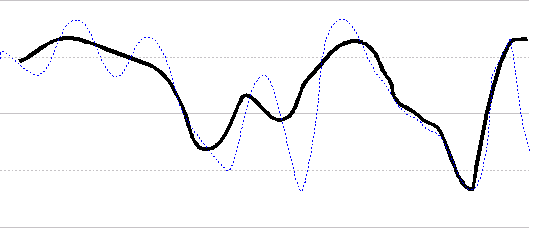
Original signal(blue), under sampled signal(black)

So, what sampling frequency should we use? Nyquist–Shannon sampling theorem states that we should sample at twice the the signal's frequency in order to reconstruct the original perfectly from the sampled version. The human ear cannot hear sounds with a frequency above 22,000 Hertz, therefore, an appropriate sampling frequency would seem to be around 44,000Hz. This is one of the reasons why music CD audio is sampled at 44,100Hz. But sampling as low as 4,000Hz is adequate to recognize human speech (telephone quality audio is about 8,000Hz)

Quantization Errors

Sampling frequency is not the only factor affecting sound quality. The precision with which we measure and store the sampled data is also very important. A signal sampled at only 4 bits per sample, will only store 16 (2⁴) different levels of amplitude, where as sampling at 16 bits per second allows a resolution of 65,536 (2¹⁶) different levels. When the sample resolution is to small, quantization errors result. The number of bits used to store the data is known as the sampling bit depth.

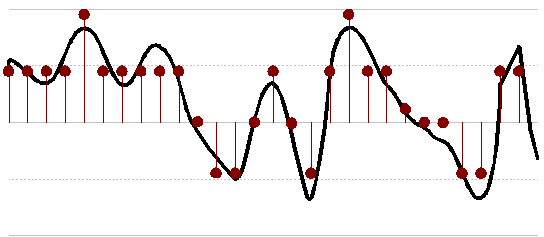
Sampling at 2 bits per sample (00₂=0 , 01₂=1 , 10₂=2, 11₂=-1)

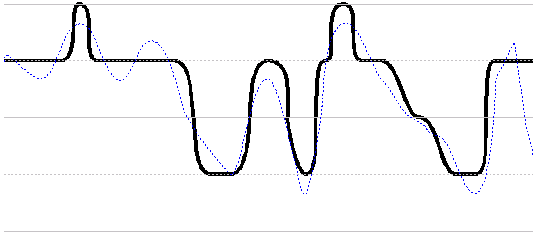
original signal (blue), result of sampling at 2 bits per sample( black)

CD audio is stored at 16 bits per sample.

The file size of the sampled data is directly related to both the sampling frequency and the bit depth. Audio sampled at 44,100Hz, with a bit depth of 16 requires 705,600 (44,100x16), bits per second of audio (about 88kBytes).

Of course MP3 files take up mush less space as they are later shrunk using sophisticated compression algorithms.

Oversampling

A CD quality audio may contain small errors unperceivable to the average human ear, but any processing or mixing effects performed on the sample will tend to magnify the errors. For this reason some digital recordings are made at frequencies as high as 192,000Hz and bits depths up to 32bits per sample, much higher than needed for digital output. This is called oversampling. The high sampling resolution allows the sample to be processed without significantly reducing the quality. After processing, the audio can be downsampled for output.